Recursive language

In mathematics, logic and computer science, a formal language (a set of finite sequences of symbols taken from a fixed alphabet) is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language. Equivalently, a formal language is recursive if there exists a Turing machine which always halts when given a finite sequence of symbols from the alphabet of the language as input and which accepts exactly those words from the alphabet of the language that are part of the language and rejects all other words. Recursive languages are also called decidable.

The concept of decidability may be extended to other models of computation. For example one may speak of languages decidable on a non-deterministic Turing machine. Therefore whenever an ambiguity is possible, the synonym for "recursive language" used is Turing-decidable language, rather than simply "decidable".

The class of all recursive languages is often called R, although this name is also used for the class RP.

This type of language was not defined in the Chomsky hierarchy of (Chomsky 1959). All recursive languages are also recursively enumerable. All regular, context-free and context-sensitive languages are recursive.

Definitions

There are two equivalent major definitions for the concept of a recursive language:

1. A recursive formal language is a recursive subset in the set of all possible words over the alphabet of the language.
2. A recursive language is a formal language for which there exists a Turing machine which will, when presented with any finite input string, halt and accept if the string is in the language, and halt and reject otherwise. The Turing machine always halts; it is known as a decider and is said to decide the recursive language.

By the second definition, any decision problem can be shown to be decidable by exhibiting an algorithm for it that terminates on all inputs. An undecidable problem is a problem that is not decidable.

Closure properties

Recursive languages are closed under the following operations. That is, if L and P are two recursive languages, then the following languages are recursive as well:

• The Kleene star
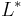
• The image φ(L) under an e-free homomorphism φ
• The concatenation
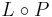
• The union
• The intersection
• The complement of L
• The set difference

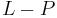
The last property follows from the fact that the set difference can be expressed in terms of intersection and complement.

References

• Michael Sipser (1997). "Decidability". Introduction to the Theory of Computation. PWS Publishing. pp. 151–170. ISBN 0-534-94728-X 
• Chomsky, Noam (1959). "On certain formal properties of grammars". Information and Control 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6. 

See also

• Recursively enumerable language
• Recursion